向量相似性解释
在自然语言处理和计算机视觉等领域,向量嵌入已被证明是一个高校的工具。比较项链嵌入并确定它们的相似性是语义检索、推荐系统和异常检测等等的重要组成部分。
在本文中,我们将更深入地了解这些相似度量是如何工作的,以直观地了解在特定用例的上下文中两个向量嵌入相似意味着什么。例如,在自然语言处理中,如果表示词义的两个向量如果在相似的上下文中使用或有着相似的含义,那么它们可能是“接近”的;在推荐系统的背景下,如果表示用户偏好的两个向量有共同的兴趣或者之前做出了相同的选择,那么它们可能是相似的。
在下面的表格中,您可以看到我们将在本文中讨论的相似性度量,以及影响度量的向量的属性。
Table 1: Similarity metrics
| Similarity Metric | Vector properties considered |
|---|---|
| Euclidean distance | Magnitudes and direction |
| Cosine similarity | Only direction |
| Dot product similarity | Magnitudes and direction |
Euclidean distance
欧几里得距离(Euclidean distance)是多维空间中两个向量之间的直线距离。
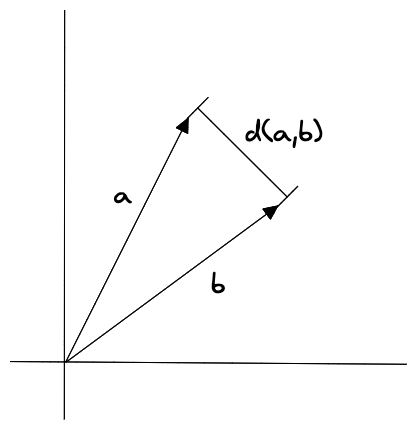
它被计算为向量相应分量之间差值平方和的平方根。以下是计算两个向量 a 和 b 之间的欧几里得距离的方程:
$$ d(a,b) = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2+…+(a_n-b_n)^2} $$
要计算两个向量 a 和 b 之间的欧几里德距离,该方程首先计算两个向量的第一个分量 $(a_1-b_1)$ 之间的差,然后计算第二个分量 $(a_2-b_2)$ 之间的差,依此类推,直到它到达第 n 个分量 $(a_n-b_n)$。然后将差值平方并相加,并取总和的平方根得出最终距离。
该度量对向量大小以及向量在空间中的相对位置敏感。这意味着具有大值的向量将比具有小值的向量具有更大的欧几里得距离,即使这些向量在其他方面相似。这可以正式表达如下:
$$d(ɑx,ɑy)=ɑd(x,y)$$
欧几里德距离是一个非常直观的相似性度量,因为它反映了被比较的向量的每个值之间的距离: 如果欧几里德距离非常小,则向量中每个坐标的值非常接近。对于点积或余弦来说,通常情况并非如此。
在大多数情况下,您不会直接将其用于深度学习模型,而是与使用更基本的向量编码方法(例如LSH(局部敏感哈希))创建的模型一起使用。换句话说,当模型没有使用特定的损失函数进行训练时,欧几里德距离是一个自然的选择。
由于欧几里得距离对大小敏感,因此当嵌入包含与事物的计数或测量有关的信息时,它会很有帮助。例如,在目标是推荐与用户之前购买的商品相似的推荐系统中:欧几里得距离可以用来衡量商品购买时间嵌入量之间的绝对差异。
Dot product Similarity
两个向量的点积相似度(Dot product Similarity)度量是通过将向量对应分量的乘积相加来计算的。向量 a 和 b 的点积计算如下:
$$ a \cdot b = \displaystyle \sum^{n}_{i=1}{a_ib_i} = a_1b_1+a_2b_2+…+a_nb_n $$
其中 a 和 b 是要比较的向量,$a_i$ 和 $b_i$ 是向量的分量。点积是通过将向量分量相乘并将结果相加来计算的。
如下所示,点积也可以表示为向量的大小与它们之间的角度的余弦的乘积:
$$ a \cdot b = |a||b|cosɑ $$
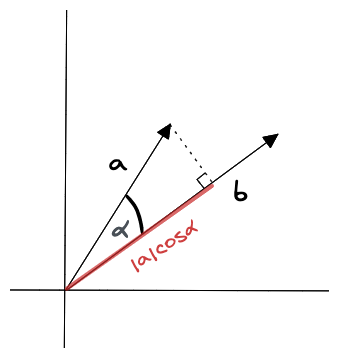
点积是标量值,这意味着它是单个数字而不是向量。如果向量之间的角度小于 90 度,则点积为正;如果向量之间的角度大于 90 度,则点积为负;如果向量正交,则点积为零。
点积会受到向量长度和方向的影响。当两个向量长度相同但方向不同时,如果两个向量指向相同方向,则点积较大;如果两个向量指向相反方向,则点积较小。想象由箭头表示的两个向量,向量 a 和向量 b 。如果向量 a 和 b 彼此指向相同方向,则 a 和 b 的点积将大于 a 和 b 指向相反方向时的点积。
您可能会遇到许多使用点积进行训练的大型语言模型 (LLM)。
在基于协同过滤和矩阵分解的推荐系统中,每个用户和每个项目(例如电影)都有一个嵌入,并且学习模型分析用户嵌入和项目嵌入之间的点积来预测用户对这个项目的评分。现在,如果两个产品的嵌入方向相同但大小不同,这可能意味着这两个产品是关于同一主题的,但幅度较大的一个产品比另一个产品更好/更受欢迎。
Cosine Similarity
余弦相似度(Cosine Similarity)是两个向量之间角度的度量。它是通过向量的点积除以它们的大小的乘积来计算的。该度量不受向量大小的影响,而仅受向量之间的角度的影响。这意味着具有大值或小值的向量只要指向相同的方向,就会具有相同的余弦相似度。以下是计算向量a和b的余弦相似度的方法:
$$ sim(a,b)= \frac{a \cdot b}{||a|| \cdot ||b||} $$
其中 a 和 b 是要比较的向量,“•”代表点积,||a|| 和||b|| 代表向量的长度。余弦相似度介于 -1 和 1 之间,其中 1 表示角度为 0(向量尽可能接近),0 表示正交,-1 表示向量指向相反方向。
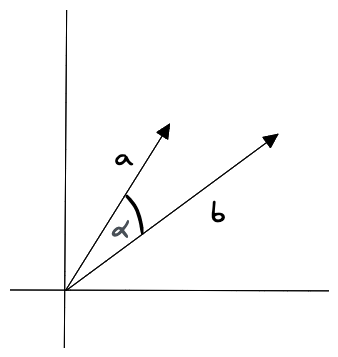
首先,该方程通过将向量的分量相乘并将结果相加来计算向量的点积。然后将点积除以向量幅值的乘积,向量幅值的乘积是通过对向量分量的平方和求平方根来计算的。
如果模型是使用余弦相似度进行训练的,则您可以使用余弦相似度或标准化并使用点积。请注意,它们在数学上是等效的。在某些情况下,归一化和使用点积更好,而在某些情况下,使用余弦相似度更好。
余弦相似度的一个示例用例是解决语义搜索和文档分类问题,因为它允许您比较向量的方向(即文档的整体内容)。同样,旨在根据用户过去的行为向用户推荐项目的推荐系统可以使用这种相似性度量。
当您的数据中向量的大小很重要并且在确定相似性时应考虑到时,余弦相似度可能不适合。例如,它不适合根据像素强度比较图像嵌入的相似度。
总结
在为索引选择相似度量时,请记住我们在本文介绍中提到的一般原则: 使用用于训练嵌入模型的相似度量。否则,您应该尝试各种其他的相似性度量,看看是否可以产生更好的结果(例如,如果您不知道嵌入模式中使用了什么相似性度量,或者创建向量的方法在生成过程中没有这样的度量)。

