向量检索简介
- 向量检索在推荐系统,图片检索,语义检索中均有⼤量应用
- 向量检索的核心是 ANN(Approximate Nearset Neighbor)问题
- 旨在向量空间中找到与查询向量近似最近邻的向量
1 何为相似
评估两个向量的相似程度有多种指标(Metrics)
- 欧式距离(Euclidean Distance)
- 余弦相似度(Cosine Similarity)
- 杰卡德相似度(Jaccard Similariy)
1.1 欧氏距离(Euclidean Distance)
即欧氏空间中,两个向量的距离
$$\sum_{i=1}^{n} (x_i - y_i)^2 = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \ldots + (x_n - y_n)^2}$$
1.2 余弦相似度(Cosine Similarity)
两个向量间的角距离
$$cos(θ)=\frac{x \cdot y}{||x|| \cdot ||y||}$$
1.3 杰卡德相似度(Jaccard Similariy)
两个向量交集占并集的比例
$$J(A,B)=\frac{|A∩B|}{|A∪B|}$$
不同的评价指标从不同的⾓度分析数据
2 向量索引算法
最直接的方法是查询向量遍历向量空间中所有的向量计算距离暴力解,缺点是计算复杂度过高。
为了加快查找的速度,几乎所有的 ANN 方法都是通过对全空间分割,将其分割成很多⼩的子空间,在搜索的时候,通过某种方式,快速锁定在某⼀(多)个子空间,然后在该(多个)子空间里做遍历。
目前主流方法分为四大类:
2.1 基于树的方法
KD 树
下面是 KD 树对全空间的划分过程,以及用树这种数据结构:
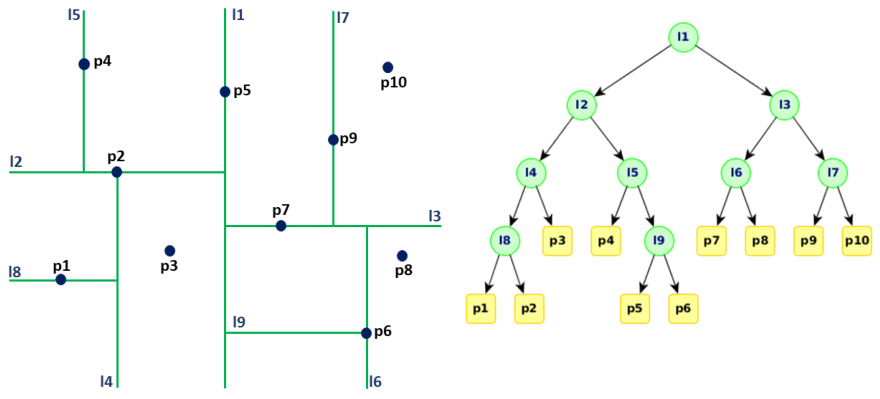
KD 树选择从哪一维度进行开始划分的标准,采用的策略是:求每一个维度的方差,然后选择方差最大的那个维度开始划分。
为何要选择方差作为维度划分选取的标准?
- 因为方差的大小可以反映数据的波动性。方差大表示数据波动性越大,选择方差最大作为划分空间标准的好处在于,可以使得所需的划分面数据最小,反映到树数据结构上,可以使得我们构建的 KD 树的树深度尽可能的小。
一般而言,在空间维度比较低的时候,KD树是比较高效的,当空间维度较高时,可以用小面即将介绍的哈希方法或者矢量量化方法。
2.2 哈希方法
通过哈希函数将连续的实值散列化为 0、1 的离散值,将向量以相似性为度量指标进行分割,将向量归类到不同的桶(cell)中。
查找时,查询向量通过哈希函数后,也会归类到相似向量的桶中,以缩小检索范围。
工程中的经典方法是局部敏感哈希(Local Sensitive Hashing, LSH),即相近的样本点对比较远的样本点更容易发生碰撞。

LSH 中重要的参数:
- K,每一个哈希表的哈希函数(空间划分)数目
- L,哈希表(每一个哈希表有 K 个哈希函数)的数目
- T,近邻哈希桶的数目,即 the number of probes
为了增加 LSH 召回率精度,在查询向量落入桶周围时,再选几个近邻的桶,以增加召回率。
通常 K T 之间要做取舍,哈希函数数目 K 越大,相应地,近邻哈希桶的数目的数目 T 也应该设置的越大,反之 K 越小,L 也可以相应的减小。
2.3 矢量量化方法
乘积量化(Product Quantization,PQ)是 Herve Jegou 在 2011 年提出的一种非常经典实用的矢量量化索引的方法,在工业界向量索引中已得到广泛的应用,并作为主要的向量索引方法,在 Fasis 中有非常高效的实现。乘积量化的核心思想是分段(划分子空间)和聚类,或者说具体应用到 ANN 近似最近邻搜索上,KMeans 是 PQ 乘积量化子空间数目为 1 的特例。PQ 乘积量化生成码本和量化的过程可以用如下图示来说明:

在训练阶段,针对 N 个训练样本,假设样本维度是 128 维,我们将其划分为 4 个子空间,则每一个子空间的维度为 32 维,然后我们在每一个子空间中,对子向量采用 K-Means 对其进行聚类(图中示意聚类为 256 类),这样每一个子空间都能得到一个码本。这样训练样本的每个子段,都可以用子样本仅使用的最短的一个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在每个子空间里逐一找到距离它们最近的类中心,然后用类中心的 id 来表示它们,即完成了待编码样本的编码。
查询阶段有两种计算距离方式:
- 对称距离,用于查询向量对应的类中心代表查询向量的位置,各个类中心代表各个类中所有点的位置,计算类中心间的距离。该方式计算快,但损失精度大。
- 非对称距离,用于查询向量本身位置,各个类中心代表各个类中所有点的位置,计算查询向量到每个类中心的位置。该方式计算较快,且损失精度较低。
同时对特征进行编码后,可以用一个相对比较短的编码来表示样本,对于内存的消耗要显著减少。
倒排 PQ 乘积量化(IVFPQ)是 PQ 乘积量化的进一步加速版。
其算法思想是,在 PQ 乘积量化之前,增加了一个粗量化过程。先对 N 个训练样本采用 KMeans 进行聚类,这里聚类的数目一般不超过 1024。在得到了聚类中心后,针对每一个样本查询向量,在对应的聚类中心再进行 PQ。
IVFPQ 中的主要参数:
- nProbe:IVF 中聚类中心数,聚类中心越多,分类越精细,查询越慢
- N:将向量平均分为 N 个子向量,子向量段数越多,分类越精细,查询越慢
- K:将每个子向量聚类为 $2^K$ 个聚类中心,聚类中心越多,分类越精细,查询越慢
2.4 基于图索引量化方法
Hierarchical Navigable Small World Graphs(HNSW)是 Yury A. Malkov 提出的一种基于图索引的方法,它是 Yury A. Malkov 在他本人之前工作 NSW 上的一种改进,通过采用分层状结构,将边按特征半径进行分层,是每个顶点在所有层中平均度数边为常数,从而将 NSW 的计算复杂度由多重对数(Ploylogarithmic)复杂度降低到了对数(logarithmic)复杂度。

每一个插入的元素对应的最大 layer 由指数衰减概率分布函数给出
mult_ = 1/log(1.0 * M_);
revSize_ = 1.0/mult_;
std:uniform_real_distribution<double> distribution(0.0,1.0);
double r = -log(distribution(level generator_)) * revSize_
- 从最大层 layer 开始贪心遍历,寻找局部最小值(最近邻)
- 将当前层找到的最近邻作为进入点(entry point)在下一层寻找局部最小。
从若干输入点(随机抽取或分割算法)开始迭代整个近邻图。整个搜索过程可以类比在地图上某个位置空间的过程:我们可以把地球当作最顶层,五大洲作为第一层,国家作为第三层,省份作为第四层……,现在如果要找海淀五道口,我们可以通过顶层以逐步递减的特征半径对其进行路由(第一层地球->第二层亚洲->第三层中国->第四层北京->海淀区),到了第 0 层后,再在局部区域做更细致的搜索。
HNSW 索引的主要参数:
- M:每个向量在图中的邻居数,M越大,图中每个顶点邻居越多,图越精细,建索引时间越长,查询时间越久,召回率越高,推荐范围 5~100
- ef_construction:构建图时,每个顶点候选的最近邻居,值越大,图越精细,建索引时间越长,查询越久,召回率越高,推荐范围 100~2000
- num_candidates:查询时,要返回的总候选最近向量数,值越大,召回率越大,查询时间越久,值不能超过 10000
- ef_search:搜索时,每个顶点候选的最近邻居数,值越大,查询时间越久,召回率越高,推荐范围 100~2000
3 Faiss 向量检索库
3.1 基础索引类型
| 索引类型 | 索引简介 | 全量检索 | 内存占用 | 召回率 | 查询速率 | 适用场景 |
|---|---|---|---|---|---|---|
| IndexFlatL2 | 计算L2距离暴力搜索 | 是 | 中等 | 准确结果 | 低 | 百万数据量 |
| IndexFlatIP | 计算内积暴力搜索 | 是 | 中等 | 准确结果 | 低 | 百万数据量 |
| IndexHNSWFlat | 使用HNSW图结构加速搜索 | 否 | 高 | 高 | 中 | 千万数据量 |
| IndexIVFFlat | 使⽤聚类缩⼩检索范围 | 否 | 中等 | 高 | 中 | 千万数据量 |
| IndexLSH | 使用哈希方法将向量二进制化加速搜索 | 否 | 低 | 高 | 中 | 千万数据量 |
| IndexScalarQuantizer | 使⽤标量量化将向量降维加速搜索 | 是 | 中等 | 中等 | 中 | 千万数据量 |
| IndexPQ | 使⽤乘积量化将向量降维加速搜索 | 是 | 低 | 中等 | 高 | 千万数据量 |
| IndexIVFScalarQuantizer | 先使用聚类在使用标量量化降维 | 是 | 中等 | 中等 | 高 | 千万数据量 |
| IndexIVFPQ | 先使用聚类再使用乘积量化降维 | 否 | 低 | 低 | 高 | 亿级数据量 |
| IndexIVFPQR | 先使用聚类再使用乘积量化降维最后重排序 | 否 | 低 | 低 | 中 | 亿级数据量 |
3.2 Faiss 索引选取
向量检索主要是检索速度和召回率之间的权衡
L2 距离暴力搜索一定可以得到精准结果,但由于全库遍历的 L2 计算,速度过慢,一般作为评估召回率的基准
目前的主流算法均从以下方面或结合优化检索速度:
- 缩小搜索范围(IVF|LAS|HNSW)
- 向量降维以减少内存使用(PQ|SQ)
但这也不可避免地在不同程度上牺牲了检索精度,每种算法的参数也决定了速度与精度间的平衡
3.2.1 需要精确结果
- 使用 IndexFlatL2 或 IndexFlatIP,不需要压缩数据或训练,常作为其他索引检索结果的基准
- 支持 GPU 加速
3.3.2 需要考虑内存限制
内存充裕
- IndexHNSWFlat 是最优选,速度与精度俱佳,然而十分消耗内存,不训练且不支持删除
- 支持 GPU 加速
需要考虑
- 可以先聚类,再使用 FlatL2 或 FlatIP
- 支持 GPU 加速
内存有限
- 使用 OPQ 降低向量维度
- 使用 PQ 量化向量
- 支持 GOU 加速(OPQ 降维在 CPU 中进行,但不是性能瓶颈)
3.3.3 需要考虑数据集大小
低于 1 百万
- IVF 使用 K-means 聚类
- 支持 CPU 加速
1 百万 - 1千万
- IVF 使用 HNSW 聚类,需要 30 × 65536 到 256 × 65536 个向量训练
- 不支持 GPU 加速
1 千万 - 1 亿
- 依然使用 HNSW 聚类,需要 30 × 262144 ($2^{18}$) 到 256 × 262144 ($2^{18}$) 个向量训练
- 只在 GPU 上训练,其他步骤在 CPU 进行,参考 train_ivf_with_gpu.ipynb
- 使用二级聚类,demo_two_level_clustering.ipynb
1 亿 - 10 亿
同上 65536 替换成 1048576 ($2^{20}$)

