像光一样搜索——HNSW算法介绍

HNSW算法介绍

本文是一篇英文翻译转载文章，主要介绍了HNSW算法。

原英文链接：https://dataman-ai.medium.com/search-like-light-speed-1-hnsw-c5b0d4665926

参考中文转载链接：https://luxiangdong.com/2023/11/06/hnsw/

我喜欢《玩具总动员》中的太空巡逻员“巴斯光年”，我也喜欢他的口号“飞向无限，飞向更远!”当我搜索信息时，我也喜欢快速找到正确的信息。这一切都是关于高速互联网和足够的带宽吗？不完全是！事实上，近乎即时搜索结果的算法是至关重要的。信息检索的速度是计算机科学中的一个重要课题。随着文本、图像或音频数据的高维嵌入式大语言模型（LLM），信息检索的速度成为数据科学的优先话题。

在这篇文章中，我将谈论:

• NLP中的向量嵌入（Embeddings）
• KNN（K-Nearest Neighbors）无法跟上速度
• 近似最近邻（ANN）感觉就像光速
• 快速搜索的初始算法
• 理解分层导航小世界图算法（HNSW）
• 代码示例：Embedding 新闻文章
• 代码示例：FAISS 用于 HNSW 搜索

NLP 中的向量嵌入

向量嵌入是自然语言处理中的一个基本概念，是对词、句子、文档、图像、音频或视频数据等对象的数字表示。这些向量嵌入被设计用来捕获它们所表示的对象的语义和上下文信息。

让我们首先描述词嵌入。2014年，一个突破性的创意 Word2Vec 出现在 NLP 中，它将单词或短语转换或“嵌入”为数值型的高维向量，称为词嵌入。这些词嵌入捕获单词之间的语义和上下文关系，使机器能够理解并使用人类语言。例如图 1 显示了三维空间中的高维向量：“铁（iron）”这个词与“火药（gunpowder）”、“金属（metals）”和“钢铁（steel）”这样的词很接近，但与“有机（organic）”、“糖（suugar）”或“谷物（grain）”等不相关的词相去甚远。

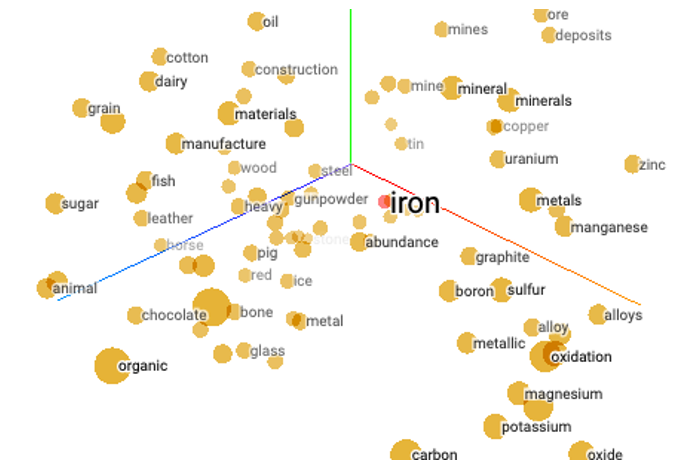
词嵌入可以表示单词之间的相似或不相似。这是一项了不起的创新。既然单词可以嵌入，为什么句子不能呢？这就是句子嵌入的诞生。句子嵌入捕捉整个句子的语义和上下文，使机器能够理解和比较句子。生成句子嵌入的常见方法是 Doc2Vec。强大的基于大语言模型（LLM）的词嵌入成为 NLP 的标准，如BERT（基于 Transformer 的双向编码器表示）、ELMo（来自语言模型的嵌入）、Llama（大型语言模型元AI），以及OpenAI的多个模型。

既然文本可以作为向量嵌入，为什么不能嵌入图像呢？这就产生了图像嵌入。卷积神经网络（CNNs）和视觉几何组（VGG）常被用于生成图像嵌入。图像嵌入使图像检索和分类成为可能。

既然图像可以作为载体嵌入，为什么我们不能嵌入音频呢？你是对的！音频嵌入可以捕捉音频数据的声学特征，并可以进行音频分类和检索。那么视频嵌入呢？它们捕捉视频分类所需的图像特征流。地理空间嵌入如何？当然。像经纬度坐标这样的地理空间数据可以嵌入到高维向量中进行信息检索。

嵌入是的一切变得简单。如果你有一篇文章，需要找到类似的文章，你只需要计算你的文章向量和其他文章向量之间的“距离”。“距离”最近的向量就是你的搜索结果。我们可以用 K-最近邻法（KNN）对吧？然而，速度是个问题。KNN 的搜索将使光年皱眉，对于巴斯光年来说，完成一次简单的搜索需要……需要不知道多少年。研究的挑战不是最近的邻居在“哪里”，而是“如何”找到他们。

K-最近邻（KNNs）无法跟上速度

假如你有一本新书，你想在图书馆内找到类似的书。k-最近邻（KNN）将浏览书架上的每一本书，并将它们从最相似到最不相似的顺序排序，以确定最相似的书。你有足够的耐心去完成这样一项繁琐的工作吗？相反，人工神经网络会先对图书馆中的书籍进行预分类和索引。要找到与你的新书相似的书，你所需要做的就是去正确的楼层，正确的区域，正确的通道找到相似的书。此外，你通常不需要对排名前 10 位的类似书籍进行精确排序，比如 100%、99% 或 95%的匹配度。这就是近似邻（ANN）的思想。

让我们来了解一下为什么人工神经网络可以更有效地搜索。

近似最近邻（ANN）感觉像光速

ANN（Approximate Nearest Neighbors）对大数据进行预索引，以方便快速搜索。在索引期间，构建数据结构以促进更快的查询。当你想找到一个查询点的近似最近邻居时，你可以将该点提供给 ANN 算法。ANN 算法首先从数据集中识别一组可能接近查询点的候选点，然后使用预构建的数据接结构选择候选点。这一步骤大大减少了需要检索接近性的数据点的数量。在候选点被选中之前，ANN 会计算每个候选点与查询点之间的实际距离（如欧几里得距离、余弦相似度）。然后根据与查询点的距离/相似度对候选点集排序。排名靠前的候选点作为近似最近邻返回。在某些情况下，你还可以设置一个距离阈值，只返回该阈值内的候选点。人工神经网络背后的关键思想是，为了显著降低计算成本，它牺牲了找到绝对最近邻的保证。这些算法的目标是在计算效率和准确性直接取得平衡。

然而，在高维空间中，过去的实验表明 ANN 并不比 KNN 节省多少时间（见[4]）。有几种创新的人工神经网络算法适用于高维空间：

最先进的快速搜索算法

这些不同的人工神经网络算法是用不同的方法，形成便于有效检索的数据结构。有三种类型的算法：基于图的、基于哈希的和基于树的：

基于图的算法创建数据的图形表示：其中每个数据点是一个节点，边表示数据点之间的接近性或相似性。最引人注目的是层次导航小世界图（HNSW）

基于哈希的算法：使用哈希函数将数据点映射到哈希值或桶。流行的算法包括：位置敏感哈希（LSH）、多索引哈希（MIH）和乘积量化

基于树的算法：将数据集划分为树状结构，以便快速搜索。流行的是 kd树、环树和随机投影树（RP树）。对于低纬空间（≤10），基于树的算法是非常有效的

有几个流行的代码库：

• Scikit-learn：它的 NearestNeighbors 类提供了一个简单的接口，可以使用 LSH 等技术进行精确和近似的最近邻搜索。
• Hnwlib：它是HNSW的Python包装器。
• faiss：该库支持多种 ANN 算法，包括 HNSW, IVFADC（带ADC量化的倒置文件）和IVFPQ（带产品量化的倒置文件）。
• Annoy（Approximate Nearest Neighbors Oh Yeah）：Annoy是一个 c++ 库，也提供了 Python 接口。
• NMSLIB（非度量空间库）：它是用 c++ 编写的，并具有 Python 包装器。它可以执行 HNSW、LSH、MIH 或随机投影树等算法。

使用上述代码库，你可以超级快速地执行搜索查询。还有一些库的变体你需要注意。这里我只提到其中的三个：

第一个是 PyNNDescent。PyNNDescent 是一个 Python 库，用于基于 NN-descent 的搜索算法，它是 LSH 的一个变体。

第二个是 NearPy。它支持多个距离度量和哈希族。

第三个是 PyKDTree。PyKDTree 是一个 Python 库，用于基于 kd 树的最近邻（KNN）搜索。虽然 kd 树更常用于精确搜索，但 PyKDTree 也可以通过一些启发式优化用于近似搜索。

此外，如果您询问哪些算法和库执行速度最好，您只需要了解 ANN-benchmark 库，专门为对人工神经网络搜索算法进行基准测试而设计。它提供了一个标准化的框架来评估算法，如 Annoy、FLANN、scikit-learn (LSHForest, KDTree, BallTree)、PANNS、NearPy、KGraph、NMSLIB(非度量空间库)、hnswlib、RPForest、FAISS、nndescent、PyNNDescent 等等。

但是“巴斯光年”不仅仅关注最近邻在哪里，还想高效地找到他们。那让我们学习第一个算法——HNSW。HNSW 通常可以在几毫秒内从数百万个数据点中找到最近邻。

了解 HNSW（分层导航小世界图）

HNSW 是一种用于高维空间中进行高效人工神经网络搜索的数据结构和算法。它是跳表（Skip Lists）和小世界（SWG）结构的拓展，可以高效地找到近似的最近邻。如果我们先学习跳表和小世界图，学习 HNSW 就会很简单。

跳表是一种用于维护已排序的元素集的数据结构，它允许进行高效的搜索、插入和删除操作。它由 William Pugh 在 1989 年发明。图（2）显示了数字 [3,6,7,9,12,17,19,21,25,26] 的排序链表。假设我们想找到目标 19。当值小于目标值时，我们向右移动。找到它需要 6 个步骤。

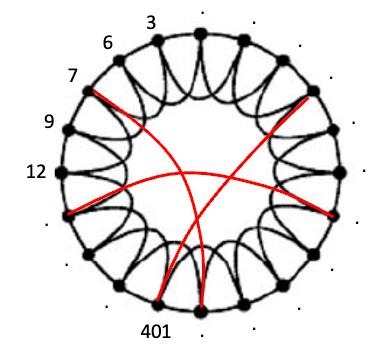
现在，如果列表中的每个其他节点都有一个指向前面第二个节点的指针，如图（3）所示，可以将这些指针视为“高速公路”。数学规则是“当数值小于目标时向右移动”。需要4个步骤才能达到19。

这些高速公路加快了搜索速度。我们可以增加更多。现在，如果列表中每三个其他节点都有一个指向前面第三个节点的指针，如图（4）所示，那么只需要 3 步就可以到达 19。

你可能会问，如何选择这些点作为”高速公路“？它们可以是预先确定的，也可以是随机的。这些节点的随机选择是 Small World 和 NHSW 中数据构建的重要步骤，我将在后面介绍。

由跳表的思路延伸到 Small World，我们来看看是怎么做的。

从跳表到 Small World

小世界网络是一种特殊的网络，在这种网络中，你可以迅速联系到网络中的其他人或点。这有点像“凯文·培根的六度”(Six Degrees of Kevin Bacon)游戏，在这个游戏中，你可以通过一系列其他演员，在不到六个步骤的时间里，将任何演员与凯文·培根联系起来。

想象一下，你有一群朋友排成一个圆圈，如图（5）所示。每个朋友都与坐在他们旁边的人直接相连。我们称它为“原始圆”。

现在，这就是奇迹发生的地方。你可以随机选择将其中一些连接人改变成圆圈中的其他人，就像图（5）中的红色连接线一样。这就像这些连接的“抢椅子”游戏。有人跳到另一把椅子上的几率用概率 p 表示。如果 p 很小，移动的人就不多，网络看起来就很像原来的圆圈。但如果 p 很大，很多人就会跳来跳去，网络就会变得有点混乱。当您选择正确的 p 值(不太小也不太大)时，红色连接是最优的。网络变成了一个小世界网络。你可以很快地从一个朋友转到另一个朋友（这就是“小世界”的特点）。

现在让我们学习从小世界网络到可导航小世界的过渡。

从 Small World 到 HNSW

现在我们要扩展到高维空间。图中的每个节点都是一个高维向量。在高维空间中，搜索速度会变慢。这是不可避免的“维度的诅咒”。HNSW 是一种高级数据结构，用于优化高维空间中的相似性搜索。

让我们看看 HNSW 如何构建图的层次结构。HNSW 从图（6）中的第 0 层这样的基础图开始。它通常是使用随机初始化来构造的数据点。

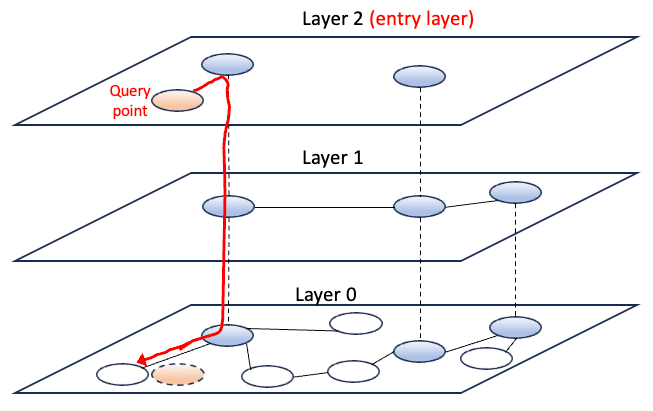
HNSW 在层次结构中的基础层之上构造附加层。每个层将有更少的顶点和边的数量。可以把高层中的顶点看作是跳跃列表中访问“高速公路”的点。你也可以将这些顶点视为游戏“Six Degrees of Kevin Bacon”中的演员 Kevin Bacon，其他顶点可以在不到六步的时间内连接到该顶点。

一旦构建了上面的层次结构，数据点就被编入索引，并准备进行查询搜索。假设查询点是橘色数据点。为了找到一个近似最近邻，HNSW 从入门级（第 2 层）开始，并通过层次结构向下遍历以找到最近的顶点。在遍历的每一步，算法会计算从查询点到当前节点邻居的距离，然后选择距离最小的邻居节点作为下一个基本节点。查询点到最近邻居之间的距离是常用的度量，如欧几里得距离或余弦相似度。当满足某个停止条件（例如距离计算次数）时，搜索终止。

现在让我们看看 HNSW 是如何构造层的。

HNSW 如何构建数据机构

HNSW 首先初始化一个空图作为数据结构的基础。该图表示一个接一个插入数据点的空间。HNSW 将数据点组织成多层。每一层表示数据结构中不同级别的粒度。层的数量是预先定义的，通常取决于数据的特征。

每个数据点会被随机分配到一个层。最高的层是最粗略的表示，随着层的向下移动，表示就会变得更精细。这个任务是用一个特定的概率分布来完成的，这个概率分布叫做指数衰减概率分布（exponential decaying probability distribution）。这种分布使得数据点到达更高层的可能性大大降低。如果你还记得跳跃列表中随机选择的数据点作为“高速公路”，这里的一些数据点是随机选择到最高层的。在后面的代码示例中，我们将看到每层中的数据点数量，并且数据点的数量在更高层中呈指数级减少。

为了在每一层内有效地构建连接，HNSW 使用贪婪搜索算法。它从顶层开始，试图将每个数据点连接到同一层内最近的邻居。一旦建立了一层中的连接，HNSW 将使用连接点作为搜索的起点继续向下扩展到下一层。构建过程一直持续到处理完所有层，并且完全构建了数据结构。

让我们简单总结一下 HNSW 中数据结构的构造。让我也参考 Malkov 和 Yashunin[3] 中的符号，并在附录中解释 HNSW 算法。你可能会发现它们有助于更明确地理解 HNSW 的算法。HNSW 声明一个空结构并逐个插入数据元素。它保持每个数据点每层最多有 M 个连接的属性，并且每个数据点的连接总数不超过最大值（Mmax）。在每一层中，HNSW 找到与新数据点最近的 K 个邻居。然后，它根据距离更新候选数据点集和找到的最近邻居列表（W）。如果 W 中的数据点数量超过了动态候选列表（ef）的大小，则该函数从 W 中删除最远的数据点。

接下来，我将向你展示代码示例。该笔记本可通过此链接获得。

代码示例

接下来，让我们使用库 FAISS 执行 HNSW 搜索。我将使用 NLP 中包含新闻文章的流行数据集。然后，我使用“SentenceTransformer”执行 Embeddings。然后，我将向你展示如何使用 HNSW 通过查询搜索类似的文章。

data

总检察长的新闻文章语料库由 A.Gulli，是一个从2000多个新闻来源收集100多万篇新闻文章的大型网站。Zhang、Zhao和LeCun在论文中构建了一个较小的集合，其中采样了“世界”、“体育”、“商业”和“科学”等新闻文章，并将其用作文本分类基准。这个数据集“ag_news”已经成为一个经常使用的数据集，可以在Kaggle、PyTorch、Huggingface和Tensorflow中使用。让我们从 Kaggle 下载数据。训练样本和测试样本分别有 12 万篇和 7600 篇新闻文章。

import pandas as pd
import numpy as np
import faiss
pd.set_option('display.max_colwidth', None)
path = "/mnt/disk8/djw/anaconda_project/content/gdrive/data"

train = pd.read_csv(path + "/train.csv")
train.shape
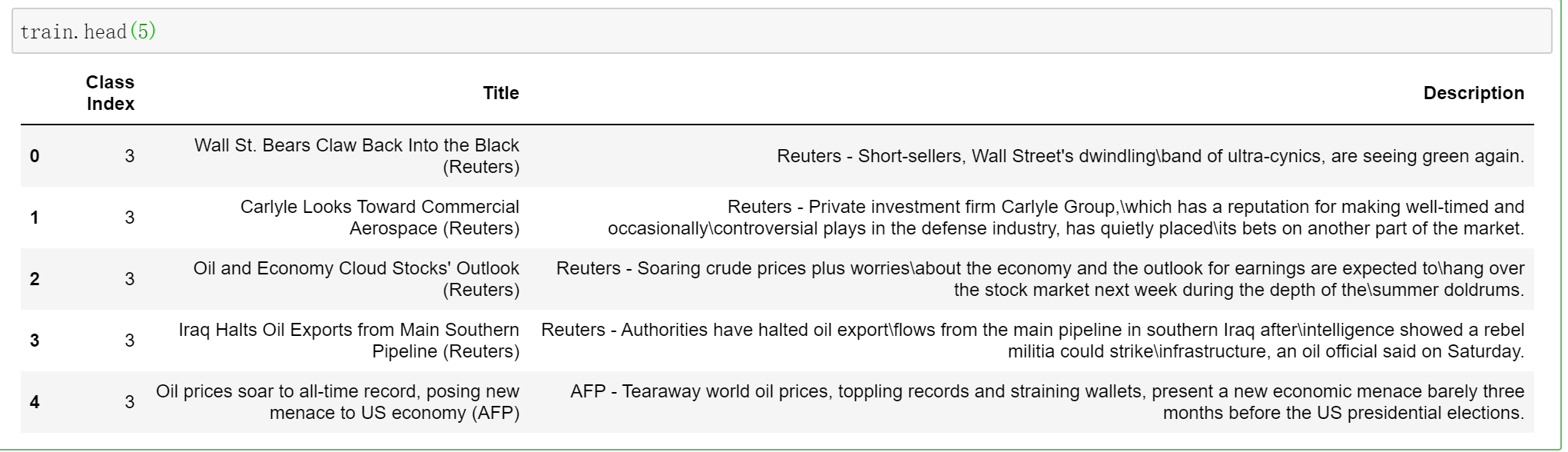
train.head(5)

输出形状为(120000,3)，列为[‘Class Index’,’Title’,’Description’]。我们对“描述”栏感兴趣。以下是排名前五的记录：

数据嵌入

出于说明的目的，我只使用10,000条记录进行Embeddings。

sentences = train['Description'][0:10000]

您需要 pip 安装”sentence_transformers”库。

!pip install sentence_transformers
from sentence_transformers import SentenceTransformer

然后让我们使用预训练模型”bert-base-nli-mean-tokens”来声明模型。在本页上有许多预先训练好的模型。

model = SentenceTransformer('bert-base-nli-mean-tokens')

然后我们将“句子”编码为“sentence_embeddings”。

sentence_embeddings = model.encode(sentences)
print(sentence_embeddings.shape)
sentence_embeddings[0:5]

输出是10,000个列表。每个列表或向量的维数为768。下面是前 5 个 Embeddings 的输出。

这有助于保存Embeddings以备将来使用。

with open(path + '/AG_news.npy', 'wb') as file:
    np.save(file, sentence_embeddings)

在上面的代码中，我使用了“npy”文件扩展名，这是 NumPy 数组文件的常规扩展名。下面是加载数据的代码:

with open (path + '/AG_news.npy', 'rb') as f:
    sentence_embeddings = np.load(f, allow_pickle=True)

有了这些 Embeddings，我们就可以在HNSW数据结构中组织它们了。

使用FAISS构建NHSW数据结构索引

您需要像下面这样 pip 安装 FAISS 库：

!pip install faiss-cpu --no-cache

我将使用 HNSWFlat(dim, m) 类来构建 HNSW。它需要预先确定的参数 dim 表示向量的维数，m 表示数据元素与其他元素连接的边数。

import faiss
m = 32
dim = 768
index = faiss.IndexHNSWFlat(dim, m)

如上所述，HNSW 指数的创建分为两个不同的阶段。在初始阶段，该算法使用概率分布来预测最上层的新数据节点。在随后的阶段中，将收集每个数据点的最近邻居，然后使用一个表示为 m（在我们的示例中为 m = 16）的值进行剪枝。整个过程迭代，从插入层开始，一直到底层。

在 HNSW 中有两个重要的参数 “efConstruction” 和 “efSearch”。这两个参数控制着索引结构构建的效率和有效性。它们帮助您在 HNSW 索引结构中的索引构造和近邻搜索操作的速度和质量之间取得平衡。

1. “efConstruction”: 这个参数在 HNSW 指数的构建过程中使用。它控制构建指数结构的速度和结构的质量之间的平衡。”efConstruction” 值决定了在构建阶段需要考虑多少候选项。较
   高的 “efConstruction” 值将产生更精确的指数结构，但也会使构建过程变慢

2. “efSearch”: 这个参数用于在 HNSW 索引中查找查询点的最近邻居。”efSearch” 值控制搜索速度和搜索质量之间的平衡。较高的 “efSearch” 值将导致更精确和穷举搜索，但也会更慢。

我们为 “efConstruction” 和 “efSearch” 设置了 40 和 16:

index.hnsw.efConstruction = 40 
index.hnsw.efSearch = 16  

我们已经声明了上面的数据结构。现在我们准备将数据 “sentence_embeddings” 一个接一个地插入到数据结构中：

index.add(sentence_embeddings)

一旦完成，我们可以检查 HNSW 数据结构中有多少数据元素：

index.ntotal

输出为 10000。它是 “sentence_embeddings” 中的数据点数。接下来，HNSW 建造了多少层？让我们来检查最大级别：

# the HNSW index starts with no levels
index.hnsw.max_level

最大级别为 2.0。这意味着有第 0、1、2 层。接下来，您可能想知道每层中数据元素的数量。让我们来看看：

levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels)

输出为 array([0,9713,280,7])。”0” 没有意义，你可以忽略它。它说第 0 层有 9713 个数据元素，第 1 层有 280 个元素，第 2 层只有 7 个元素。注意，9713 + 280 + 7 = 10000。您是否发现，较高层的数据元素数量比前几层呈指数级减少？这是因为数据元素的层分配采用指数衰减概率分布。

FAISS为HNSW搜索示例

假设我们的搜索查询是“经济繁荣与股市（economic booming and stock market）”。我们希望找到与我们的搜索查询相关的文章。我们将首先嵌入搜索查询：

qry1 = model.encode(["economic booming and stock market"])

使用代码 index.search()，搜索过程非常简单。这里 k 是最近邻居的个数。我们将其设置为 5，即返回 5 个邻居。index.search()函数返回两个值 “d” 和 “I”。

• “d”: 查询向量与 k 个最近邻之间的距离列表。默认的距离度量是欧几里得度量。
• “i”: 索引中 k 个最近邻居的位置对应的索引列表。这些索引可以用来查找数据集中的实际数据点。

%%time
k=5
d, I = index.search(qry1, k)
print(I)
print(d)

索引列表的输出是[[6412 6394 9103 3813 1467]]。我们将使用这些索引打印出搜索结果。

注意，我使用 “%%time” 来度量执行时间。它输出

CPU times: user 812 ms, sys: 42.6 ms, total: 855 ms

这意味着搜索只需要几百毫秒。这确实是令人难以置信的快!

距离输出列表为：[[155.64159 169.03458 183.2863 190.07074 194.54048]]

for i in I[0]:
  print(train['Description'][i])

这些文章都是关于经济和股票市场的新闻。搜索速度以毫秒计非常快。这不仅仅是结果在哪里的问题，而是如何快速得到结果的问题，不是吗?

您可以通过此链接下载笔记本进行上述搜索。

总结

我希望这篇文章能帮助你理解近似近邻（ANN），以及它是如何提供高效搜索的。本文介绍了不同的人工神经网络算法，包括基于图的 HNSW，基于哈希的 LSH 或乘积量化，以及基于树的 KD-Trees。是如何构建它的数据结构并逐个插入数据元素的。这篇文章演示了如何使用 FAISS 库构建用于查询搜索的 HNSW。

附录

在 Malkov 和 Yashunin [3]的论文中，算法 1 到 5 伪代码中介绍了 HNSW 算法。伪代码给出了算法的具体定义。我在伪代码中加入了以下的描述，可能会帮助一些读者更轻松地理解 HNSW。算法 1、算法 2、算法 3 和算法 4 中的任意一个，都可被用来构建数据结构。但一旦数据结构完成，任何未来的查询搜索只使用算法 5。

• 算法1:”INSERT”函数构造数据结构
• 算法2:”SEARCH-LAYER”函数计算 KNN 并存储邻居
• 算法3:”SEARCH-NEIGHBORS-SIMPLE”函数是一种选择邻居的简单方法
• 算法4:”SELECT-NEIGHBORS-HEURISTIC”函数是一种更复杂的选择邻居的方法
• 算法5:”KNN-SEARCH”函数进行查询搜索

算法一：INSERT()

Algorithm 1: INSERT()

INSERT(hnsw, q, M, Mmax, efConstruction, mL)
Input: multilayer graph hnsw, new element q, number of established
connections M, maximum number of connections for each element
per layer Mmax, size of the dynamic candidate list efConstruction, nor-
malization factor for level generation mL
Output: update hnsw inserting element q

1 W ← ∅ // list for the currently found nearest elements
2 ep ← get enter point for hnsw
3 L ← level of ep // top layer for hnsw
4 l ← ⌊-ln(unif(0..1))∙mL⌋ // new element’s level
5 for lc ← L … l+1
6 W ← SEARCH-LAYER(q, ep, ef=1, lc)
7 ep ← get the nearest element from W to q
8 for lc ← min(L, l) … 0
9 W ← SEARCH-LAYER(q, ep, efConstruction, lc)
10 neighbors ← SELECT-NEIGHBORS(q, W, M, lc) // alg. 3 or alg. 4
11 add bidirectionall connectionts from neighbors to q at layer lc
12 for each e ∈ neighbors // shrink connections if needed
13 eConn ← neighbourhood(e) at layer lc
14 if │eConn│ > Mmax // shrink connections of e
// if lc = 0 then Mmax = Mmax0
15 eNewConn ← SELECT-NEIGHBORS(e, eConn, Mmax, lc)
// alg. 3 or alg. 4
16 set neighbourhood(e) at layer lc to eNewConn
17 ep ← W
18 if l > L
19 set enter point for hnsw to q
20 return hnsw

它在多层图中插入一个新元素 q，保证每个元素每层最多有 M 个连接，并且每个元素的连接总数不超过 Mmax。该算法还保证了连通元素之间的距离不大于某个最大距离，并且每层的连通数是均衡的。具体步骤如下:

1. W ← ∅：初始化一个空列表 W 来存储当前找到的最近的元素。
2. ep ← get enter point for hnsw：获取多层图 HNSW 的进入点（即初始点）
3. L ← level of ep：获取进入点 ep 的级别。
4. l ← ⌊-ln(unif(0..1))∙mL⌋：为新元素 q 生成一个介于 0 和 mL 之间的随机级别，其中 mL 是级别生成的归一化因子。
5. for lc ← L … l+1：循环从 L 到 l + 1 的层。
6. W ← SEARCH-LAYER(q, ep, ef=1, lc)：使用进入点 ep 和最大距离 ef=1 在 lc 层中搜索离 q 最近的元素。将找到的元素存储在列表 W 中。
7. ep ← get the nearest element from W to q：取 W 到 q 最近的元素。
8. for lc ← min(L, l) … 0：循环遍历从 min(L, l) 到 0 的层。
9. W ← SEARCH-LAYER(q, ep, efConstruction, lc)：使用进入点 ep 和最大距离 efConstruction 在 lc 层中搜索离 q 最近的元素。将找到的元素存储在列表 w 中。
10. neighbors ← SELECT neighbors (q, W, M, lc)：选择 W 到 q 最近的 M 个邻居，只考虑 lc 层的元素。
11. add bidirectionall connectionts from neighbors to q at layer lc： 在 lc 层的 q 和选定的邻居之间添加双向连接。
12. 12~14：对于每个e∈neighbors，如果需要收缩连接，对于 q 的每个邻居 e，检查 e 的连接数是否超过 Mmax。如果超过，使用SELECT neighbors (e, eConn, Mmax, lc) 选择一组新的邻居来收缩 e 的连接，其中 eConn 是 e 在 lc 层的当前连接集。
13. eNewConn ← SELECT-NEIGHBORS(e, eConn, Mmax, lc)：为 e 选择一组新的邻居，只考虑 lc 层的元素，保证连接数不超过 Mmax。
14. set neighbourhood(e) at layer lc to eNewConn：将层lc 的 e 的连接集更新为新的集合 eNewConn。
15. ep ← W：设置 hnsw 的进入点为 q。
16. if l > L，将 hnsw 的起始点设为 q，因为新元素 q 现在是图的一部分。
17. 返回更新后的多层图 hnsw。

算法二：SEARCH-LAYER()

该算法对 HNSW 数据结构进行 k 近邻搜索，以查找特定层 lc 中与查询元素 q 最近的 k 个元素。然后，根据查询元素 q 与候选元素 C 和 e 之间的距离更新候选元素集合 C 和找到的最近邻居列表 W，最后，如果 W 中的元素个数超过动态候选列表 ef 的大小，则函数移除从 W 到 q 的最远元素。

Algorithm 2: SEARCH-LAYER()

SEARCH-LAYER(q, ep, ef, lc)
Input: query element q, enter points ep, number of nearest to q ele-
ments to return ef, layer number lc
Output: ef closest neighbors to q
1 v ← ep // set of visited elements
2 C ← ep // set of candidates
3 W ← ep // dynamic list of found nearest neighbors
4 while │C│ > 0
5 c ← extract nearest element from C to q
6 f ← get furthest element from W to q
7 if distance(c, q) > distance(f, q)
8 break // all elements in W are evaluated
9 for each e ∈ neighbourhood(c) at layer lc // update C and W
10 if e ∉ v
11 v ← v ⋃ e
12 f ← get furthest element from W to q
13 if distance(e, q) < distance(f, q) or │W│ < ef
14 C ← C ⋃ e
15 W ← W ⋃ e
16 if │W│ > ef
17 remove furthest element from W to q
18 return W

以下是上述代码的步骤：

1. 初始化变量 v 为当前的入口点 ep。
2. 初始化集合 C 为当前候选集合。
3. 初始化一个空列表 W 来存储找到的最近邻。
4. 循环直到候选集合 C 中的所有元素都被计算完毕。
5. 从候选元素集合 C 中提取离查询元素 q 最接近的元素 c。
6. 获取从找到的最近邻 W 到查询元素 q 的列表中最远的元素 f。
7. 如果 c 到 q 的距离大于 f 到 q 的距离：
8. 然后打破这个循环。
9. 对于 lc 层 c 邻域内的每个元素 e：
10. 如果 e 不在访问元素 v 的集合中，则：
11. 将 e 添加到访问元素 v 的集合中。
12. 设 f 为从 W 到 q 的最远的元素。
13. 如果 e 和 q 之间的距离小于等于 f 和 q 之间的距离，或者 W 中的元素个数大于等于 ef（动态候选列表的大小），则：
14. 将候选集 C 更新为 C∈e。
15. 将发现的最近邻居 W 的列表更新为 W∈e。
16. 如果W中的元素个数大于等于 ef，则:
17. 移除从 W 到 q 的最远的元素。
18. 返回找到的最近邻居 W 的列表。

算法三：SELECT-NEIGHBORS-SIMPLE()

这是一个简单的近邻选择算法，它以一个基本元素 q、一组候选元素 c 和若干近邻 m 作为输入。它从候选元素 c 的集合中返回 m 个离 q 最近的元素。

Algorithm 3: SELECT-NEIGHBORS-SIMPLE()

SELECT-NEIGHBORS-SIMPLE(q, C, M)
Input: base element q, candidate elements C, number of neighbors to
return M
Output: M nearest elements to q
return M nearest elements from C to q

步骤如下：

1. 初始化一个空集 R 来存储选中的邻居。
2. 初始化一个工作队列 W 来存储候选元素。
3. 如果设置了 extendCandidates 标志（即true），则通过将 C 中每个元素的邻居添加到队列 W 来扩展候选列表。
4. 而 W 的大小大于 0，R 的大小小于 M：
5. 从 W 到 q 中提取最近的元素 e。
6. 如果 e 比 R 中的任何元素更接近 q，把 e 加到 R 中。
7. 否则，将 e 添加到丢弃队列 Wd 中。
8. 如果设置了 keepPrunedConnections 标志（即true），则从 Wd 添加一些丢弃的连接到R。
9. 返回 R。

算法四：SELECT-NEIGHBORS-HEURISTIC()

这是一个更复杂的近邻选择算法，它接受一个基本元素 q、一组候选元素 c、一些邻居 m、一个层数 lc 和两个标志 extend candidates 和 keepPrunedConnections 作为输入。它返回启发式选择的 m 个元素。

Algorithm 4: SELECT-NEIGHBORS-HEURISTIC()

SELECT-NEIGHBORS-HEURISTIC(q, C, M, lc, extendCandidates, keep-
PrunedConnections)
Input: base element q, candidate elements C, number of neighbors to
return M, layer number lc, flag indicating whether or not to extend
candidate list extendCandidates, flag indicating whether or not to add
discarded elements keepPrunedConnections
Output: M elements selected by the heuristic
1 R ← ∅
2 W ← C // working queue for the candidates
3 if extendCandidates // extend candidates by their neighbors
4 for each e ∈ C
5 for each eadj ∈ neighbourhood(e) at layer lc
6 if eadj ∉ W
7 W ← W ⋃ eadj
8 Wd ← ∅ // queue for the discarded candidates
9 while │W│ > 0 and │R│< M
10 e ← extract nearest element from W to q
11 if e is closer to q compared to any element from R
12 R ← R ⋃ e
13 else
14 Wd ← Wd ⋃ e
15 if keepPrunedConnections // add some of the discarded
// connections from Wd
16 while │Wd│> 0 and │R│< M
17 R ← R ⋃ extract nearest element from Wd to q
18 return R

步骤如下：

1. 初始化三个队列：R 用于选择的邻居，W 用于工作的候选，Wd 用于丢弃的候选。
2. 设置 R 的大小为 0，W 的大小为 C 的大小。
3. 如果 extendCandidates 被设置（即，true）：
4. 对于 C 中的每个元素 e：
5. 对于第 lc 层 e 的每一个邻居 eadj：
6. 如果 eadj 不在 W 中，则在 W 中添加它。
7. 而 W 的大小大于 0，R 的大小小于 M：
8. 从 W 到 q 中提取最近的元素 e。
9. 如果 e 比 R 中的任何元素更接近 q，把 e 加到 R 中。
10. 否则，将 e 加到 Wd。
11. 如果设置了 keepPrunedConnections（即true）：
12. 而 Wd 的大小大于 0，R 的大小小于 M：
13. 从 Wd 到 q 中提取最近的元素 e。
14. 如果 e 比 R 中的任何元素更接近 q，就把 e 加到 R 中。
15. 返回 R。

算法五：K-NN-SEARCH()

这个搜索算法与算法1基本相同。

Algorithm 5: K-NN-SEARCH()

K-NN-SEARCH(hnsw, q, K, ef)
Input: multilayer graph hnsw, query element q, number of nearest
neighbors to return K, size of the dynamic candidate list ef
Output: K nearest elements to q
1 W ← ∅ // set for the current nearest elements
2 ep ← get enter point for hnsw
3 L ← level of ep // top layer for hnsw
4 for lc ← L … 1
5 W ← SEARCH-LAYER(q, ep, ef=1, lc)
6 ep ← get nearest element from W to q
7 W ← SEARCH-LAYER(q, ep, ef, lc =0)
8 return K nearest elements from W to q

步骤如下：

1. 初始化一个空集合 W（当前最近元素的集合），并将进入点 ep 设置为网络的顶层。
2. 设置进入点 ep 的级别设置为顶层 L。
3. 对于每一层 lc，从 L 到 1（即从顶层到底层）:
4. 使用查询元素 q 和当前最近的元素 W 搜索当前层，并将最近的元素添加到 W 中。
5. 将进入点 ep 设置为 W 到 q 最近的元素。
6. 使用查询元素 q 和当前最近的元素 W 搜索下一层，并将最近的元素添加到 W 中。
7. 返回 W 中最接近的 K 个元素作为输出。

参考文献

• [1] Pugh, W. (1990). Skip lists: A probabilistic alternative to balanced trees. Communications of the ACM, 33(6), 668–676. doi:10.1145/78973.78977. S2CID 207691558.
• [2] Xiang Zhang, Junbo Zhao, & Yann LeCun. (2015). Character-level Convolutional Networks for Text Classification
• [3] Yu. A. Malkov, & D. A. Yashunin. (2018). Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs.
• [4] Aristides Gionis, Piotr Indyk, Rajeev Motwani, et al. 1999. Similarity search in high dimensions via hashing. In Vldb, Vol. 99. 518–529.