量化索引:Product Quantization 乘积量化
引言
Product Quantization,国内有人直译为乘积量化,这里的乘积量化是指笛卡尔积(Cartesian product),意思是指把原先的向量空间分解为若干个低维向量空间的笛卡尔积,并对分解得到的低纬向量空间的分别做量化(quantization)。这样每个向量就能由多个低纬空间的量化 code 组合表示。为简洁描述起见,下文用 PQ 作为 Product Quantization 的简称。
The idea is to decomposes the space into a Cartesian product of low dimensional subspaces and to quantize each subspace separately. A vector is represented by a short code composed of its subspace quantization indices.
近几年,深度学习技术被广泛用于图像识别、语音识别、自然语言处理等领域,能够把每个实体(图像、语音、文本)转换为对应的 embedding 向量。一般来说,相似的实体转换得到的 embedding 向量也是相似的。对于相似搜索问题,最简单的想法是暴力穷举法,如果全部实体的个数是 N,N 是千万量级甚至是上亿的规模,每个实体对应的向量是 D,那么当要从这个实体集合中寻找某个实体的相似实体,暴力穷举的计算复杂度是 O(ND),这是一个非常大的计算量,该方法显然不可取。所以对大数据量下高维度数据的相似搜索场景,我们就需要一些高效的相似搜索技术,而 PQ 就是其中一类方法。
Product Quantization
定义
Product Quantization 是将每个数据集向量转换为短内存高效表示(称为 PQ 代码)的过程。不是完全保留所有向量,而是存储它们的简短表示。同时,PQ 是一种有损压缩算法,预测精度较低,但在实际应用中效果还不错。
In general, quantization is the process of mapping infinite values to discrete ones.
训练
首先,该算法将每个向量划分为几个相等的部分——子向量。所有数据集向量的各个部分形成独立的子空间,并分别进行处理。然后对向量的每个子空间执行聚类算法。通过这样做,在每个子空间中创建了几个质心。每个子向量都使用它所属质心的 ID 进行编码。此外,存储所有质心的坐标以供以后使用。
Subspace centroids are also called quantized vectors.
In product quantization, a cluster ID is often referred to as a reproduction value.
注意: 在下图中,一个矩形表示一个包含多个值的向量,而一个正方形表示一个数字。
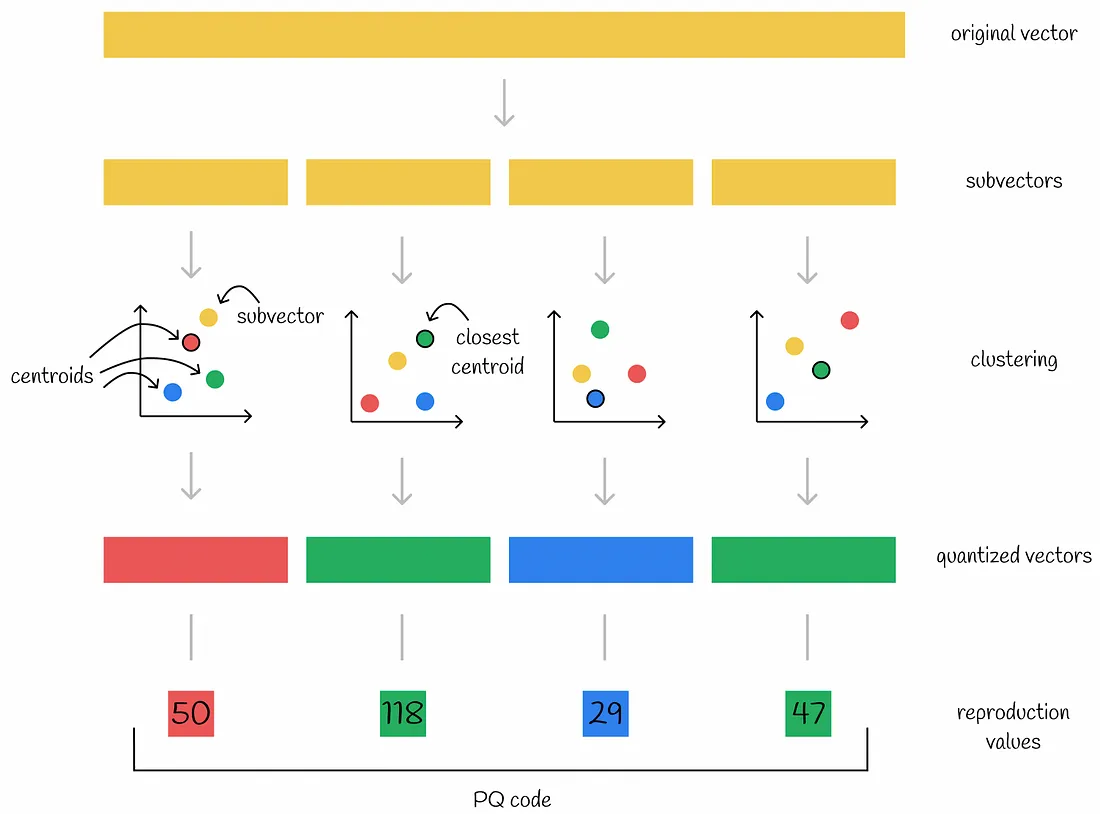
因此,如果一个原始向量被分成 n 个部分,那么它就可以用 n 个数字进行编码——每个子向量的各个质心的 ID。通常,为了更有效地使用内存,创建的质心 k 的数目通常被选为 2 的幂。这样,存储编码向量所需的内存是 n * log(k) bits。
The collection of all centroids inside a subspace is called a codebook. Running n clustering algorithms for all subspaces produces n separate codebooks.
压缩示例
设想一个大小为 1024 的存储浮点数(32bits)的原始向量被分成 n = 8 个子向量,其中每个子向量由 k = 256 个簇中的一个进行编码。因此,编码单个集群的 ID 将需要 $\log_2 256=8 bits$。让我们比较两种情况下向量表示的内存大小:
- 原始向量: 1024 * 32 bits = 4096 bytes
- 编码向量: 8 * 8 bits = 8 bytes
最终的压缩是 512 倍! 这是产品量化的真正威力。
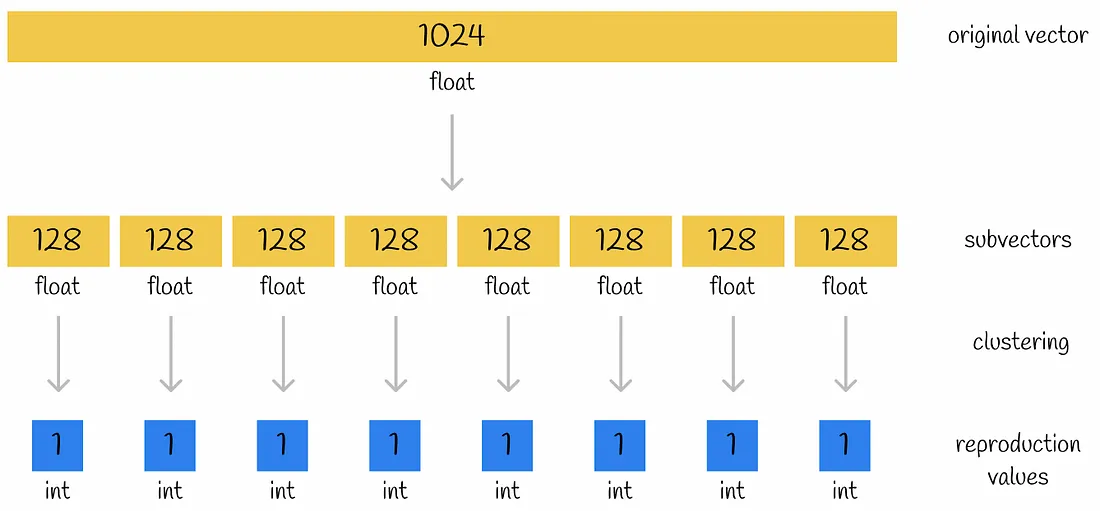
以下是一些重要的注意事项:
- 该算法可以在一个向量子集上进行训练(例如,创建聚类),并用于另一个向量子集:训练完算法后,将传递另一个向量数据集,然后使用每个子空间已构造的质心对新向量进行编码。
- 通常,选择 k-means 作为聚类算法。它的优点之一是集群的数量 k 是一个超参数,可以根据内存使用需求手动定义。
推理
为了更好地理解,让我们首先看看几种朴素方法,并找出它们的缺点。这也将帮助我们认识到为什么它们不应该被正常使用。
朴素方案
第一种朴素的方法包括通过连接每个向量相应的质心来解压缩所有向量。之后,可以计算从查询向量到所有数据集向量的 L2 距离(或其他度量)。显然,这种方法是可行的,但是非常耗时,因为要对高维解压向量进行暴力搜索和距离计算。
另一种可能的方式是将查询向量分割成子向量,并基于其 PQ 码计算从每个查询子向量到数据库向量的各个量化向量的距离之和。因此,这里再次使用了暴力搜索技术,并且距离计算仍然需要原始向量维数的线性时间,就像前面的情况一样。
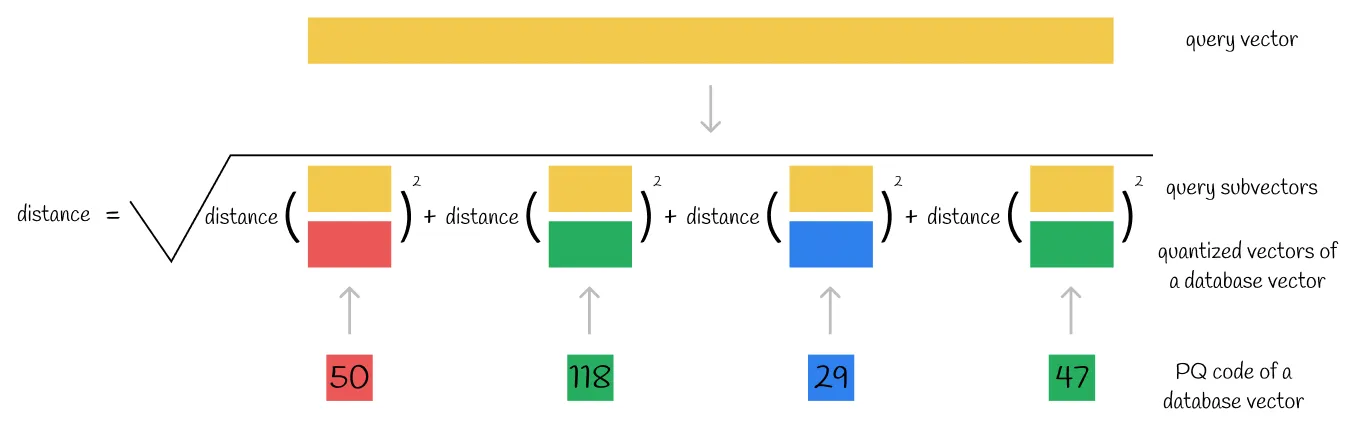
另一种可能的方法是将查询向量编码成 PQ 码。然后这个 PQ 码被直接用来计算到所有其他 PQ 码的距离。将距离最短的数据集向量与相应的 PQ 码作为查询的最近邻。这种方法比前两种方法更快,因为它总是计算低维 PQ 码之间的距离。然而,PQ 码是由群集 ID 组成的,这种群集 ID 没有多少语义意义,可以看作是一个明确用作实变量的范畴变量。显然,这是一个不好的做法,这种方法可能会导致预测质量差。
最佳方案
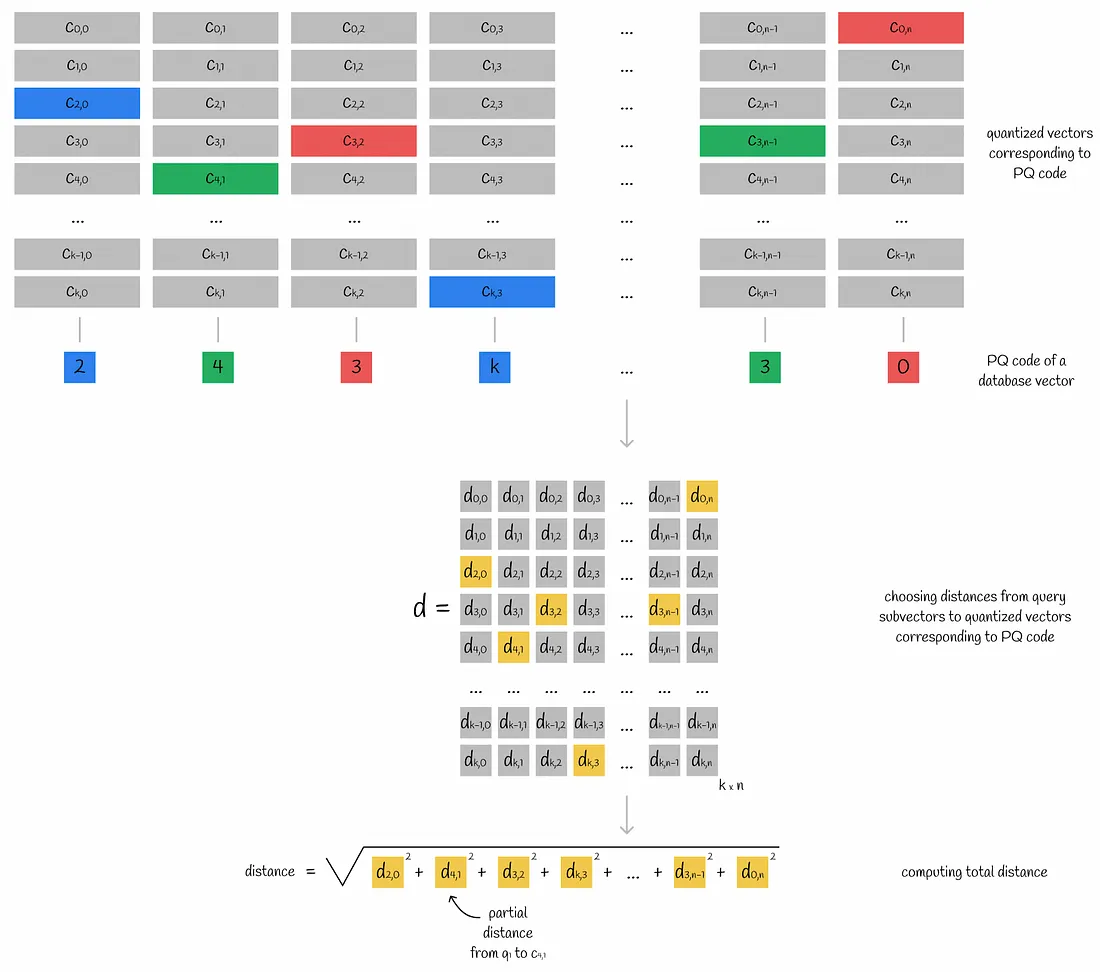
查询向量被划分为子向量。对于每个子向量,计算到相应子空间的所有质心的距离。最终,该信息存储在表 d 中。
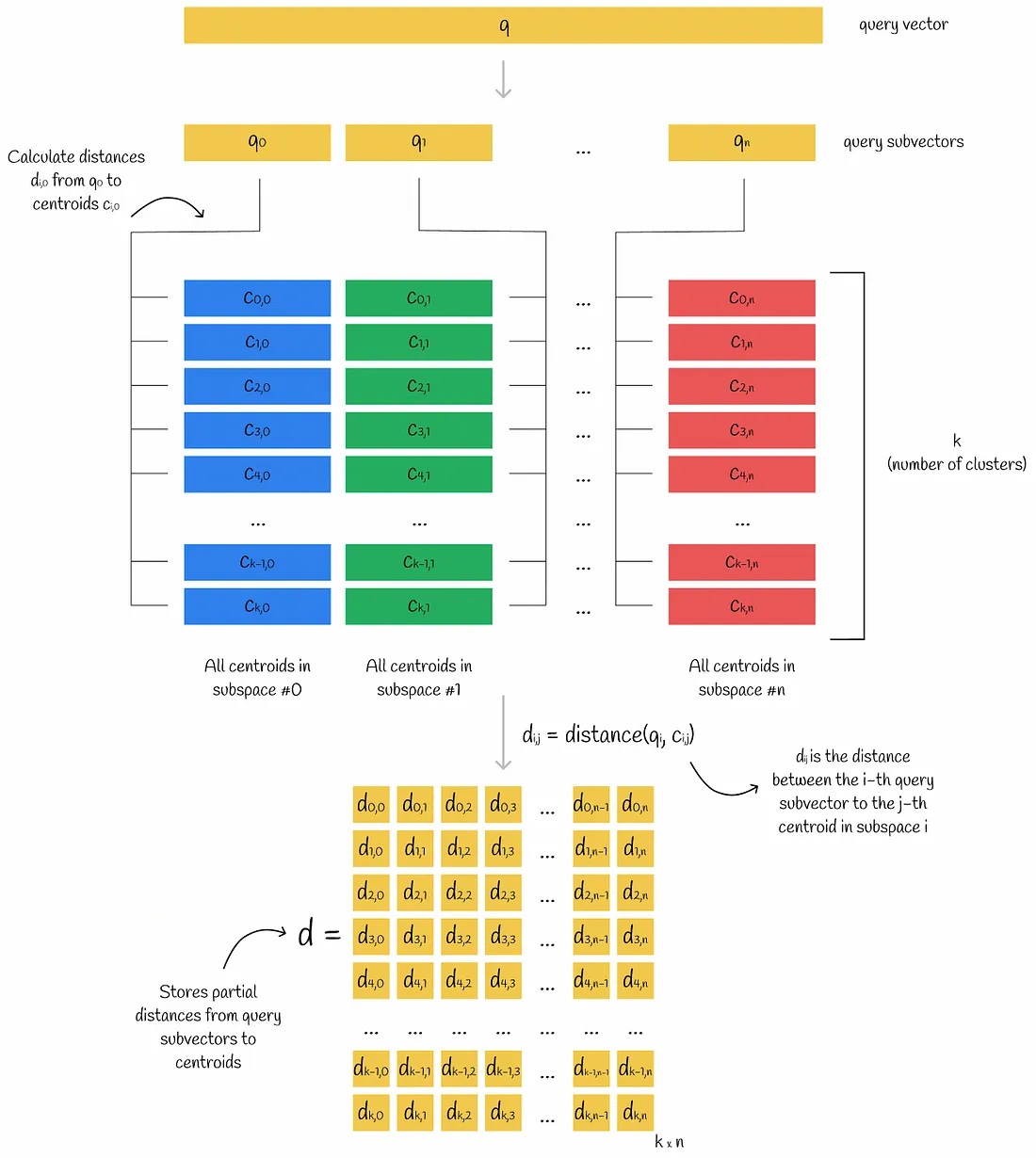
Calculated subvector-to-centroid distances are often referred to as partial distances.
通过使用这个子向量到质心距离表 d,可以很容易地通过其 PQ 码获得从查询到任何数据库向量的近似距离:
- 对于数据库向量的每个子向量,找到最近的质心 j (通过使用来自 PQ 码的映射值) ,并获得从该质心到查询子向量 i(通过使用计算的矩阵 d)的偏距(partial distance) d[i][j]。
- 所有的偏距均被平方并求和。通过对该值求平方根,即可获得近似的欧氏距离。如果您还想知道如何获得其他度量的近似结果,请导航到“其他距离度量的近似值”部分。
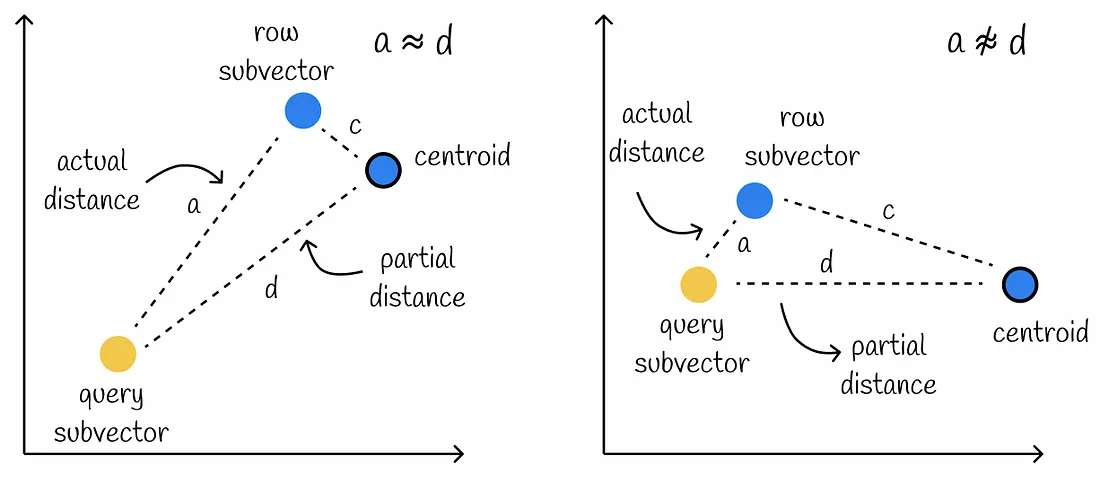
Using this method for calculating approximate distances assumes that partial distances d are very close to actual distances a between query and database subvectors.
然而,这个条件可能不被满足,特别是当数据库子向量与其质心之间的距离 c 很大时。在这种情况下,计算会导致精度降低。
在获得所有数据库行的近似距离后,我们搜索具有最小值的向量。这些向量将是查询的最近邻。
其他距离度量的近似
到目前为止,我们已经研究了如何通过使用偏距来近似欧几里得度量。让我们将这个规则推广到其他度量标准。
想象一下我们想要计算一对向量之间的距离度量。如果我们知道度量的公式,我们可以直接应用它来得到结果。但是有时候我们可以通过以下方式分部分的做:
- 两个向量被分成 n 个子向量
- 对于每对各自的子向量,计算距离度量
- 然后将计算出的 n 个度量结合起来生成原始向量之间的实际距离
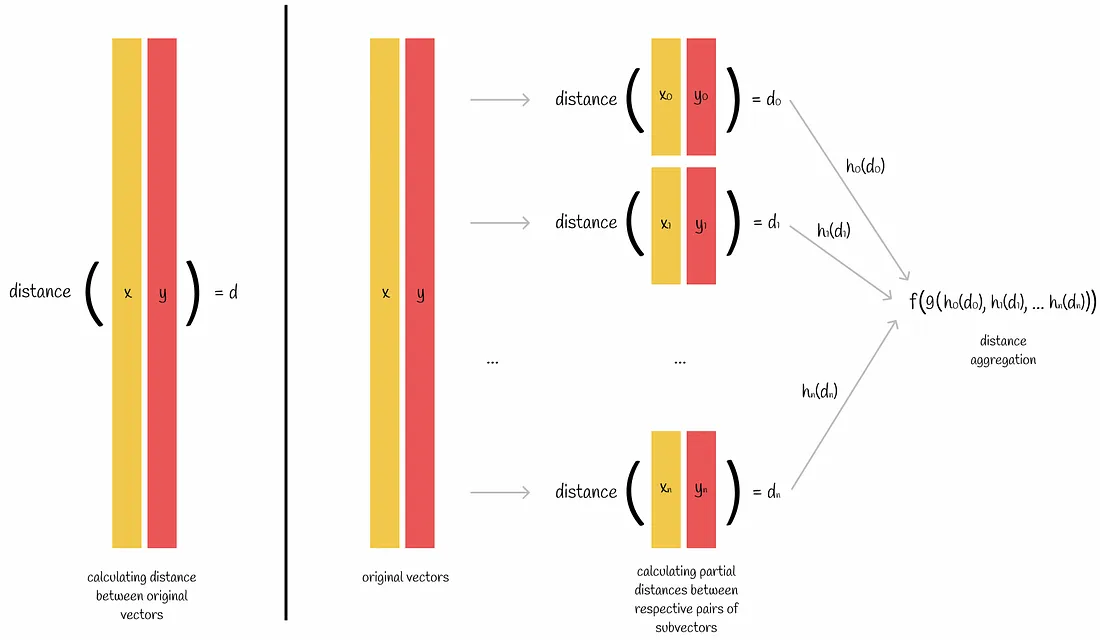
欧几里得度量是一个可以按部分计算的度量标准的例子。根据上图,我们可以选择聚合函数 $h(z)=z^2$,$g(z_0,z_1…,z_n)=sum(z_0,z_1,…,z_n)$ 和 $f(z)=\sqrt{z}$。
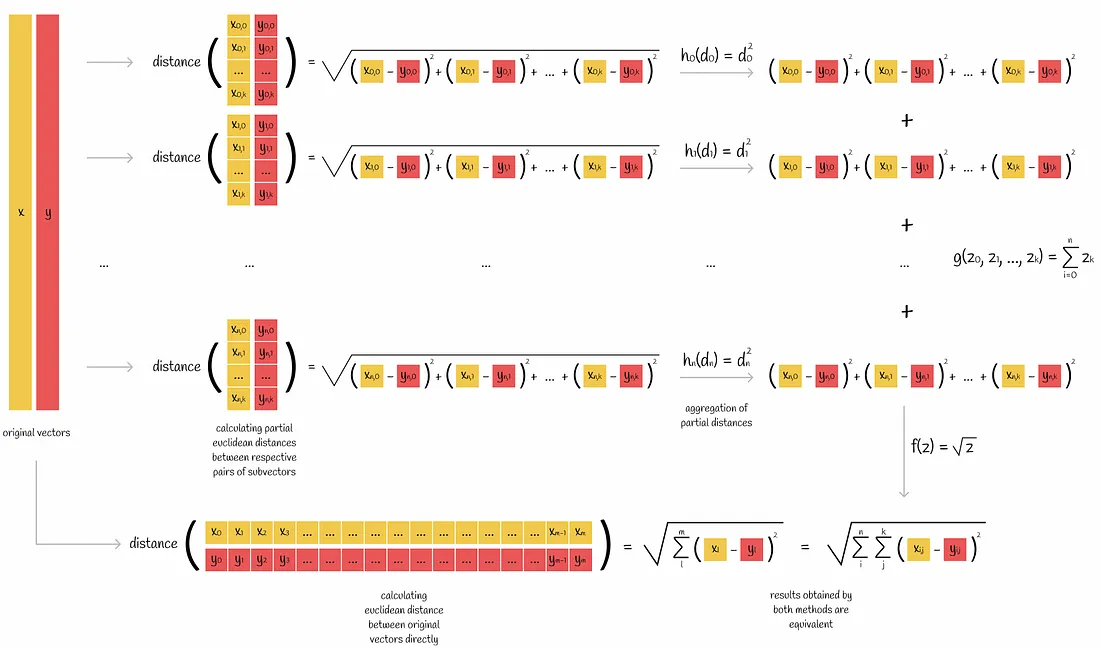
内积是这种度量的另一个例子,其聚合函数 $h(z)=z$,$g(z_0,z_1…,z_n)=sum(z_0,z_1,…,z_n)$ 和 $f(z)=z$。
在乘积量化的背景下,这是一个非常重要的属性,因为在推理过程中,算法按部分计算距离。这意味着,使用不具有此属性的指标进行乘积量化会出现更多问题,例如余弦距离
演示
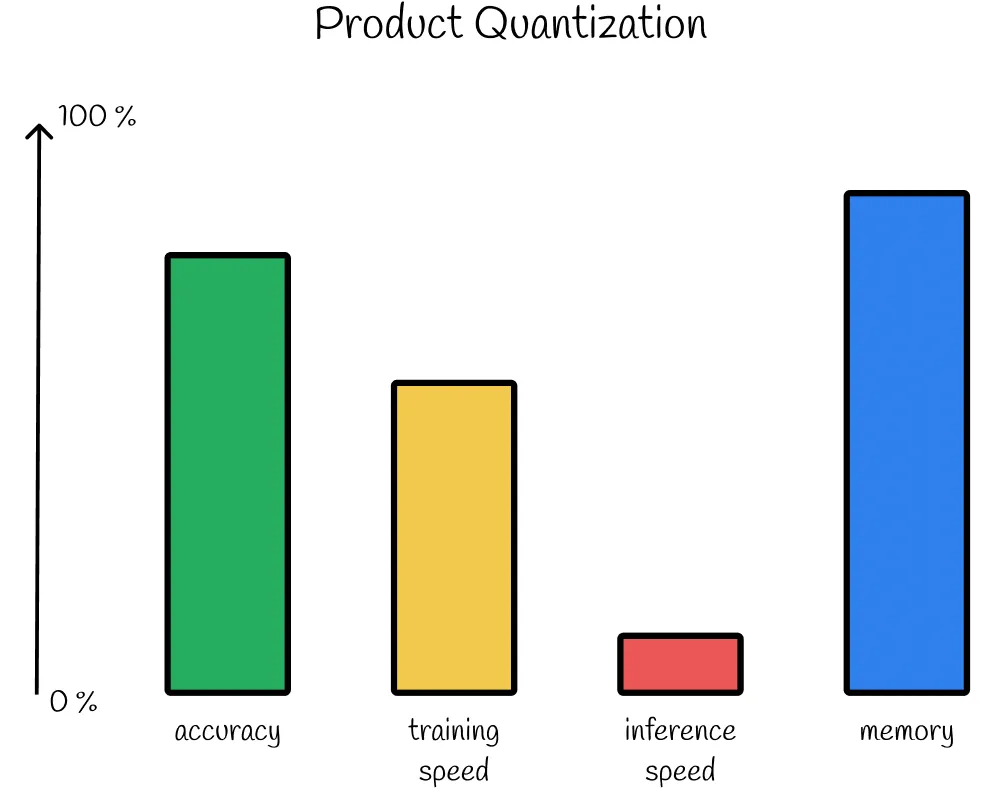
乘积量化的主要优点是对存储为短 PQ 码的数据库向量进行大规模压缩。对于某些应用程序,这样的压缩率甚至可能高于 95%!然而,除了 PQ 码之外,还需要存储包含各子空间量子化向量的 k×n 矩阵 d。
Product quantization is a lossy-compression method, so the higher the compression is, the more likely that the prediction accuracy will decrease.
建立一个有效的表示系统需要训练多个聚类算法。除此之外,在推理过程中,k*n 的偏距需要以蛮力的方式计算,并为每个数据库向量求和,这可能需要一些时间。
Faiss 执行
Faiss (Facebook AI Search Similarity) is a Python library written in C++ used for optimised similarity search. This library presents different types of indexes which are data structures used to efficiently store the data and perform queries.
基于来自 Faiss 文档的信息,我们将看到如何使用 PQ。
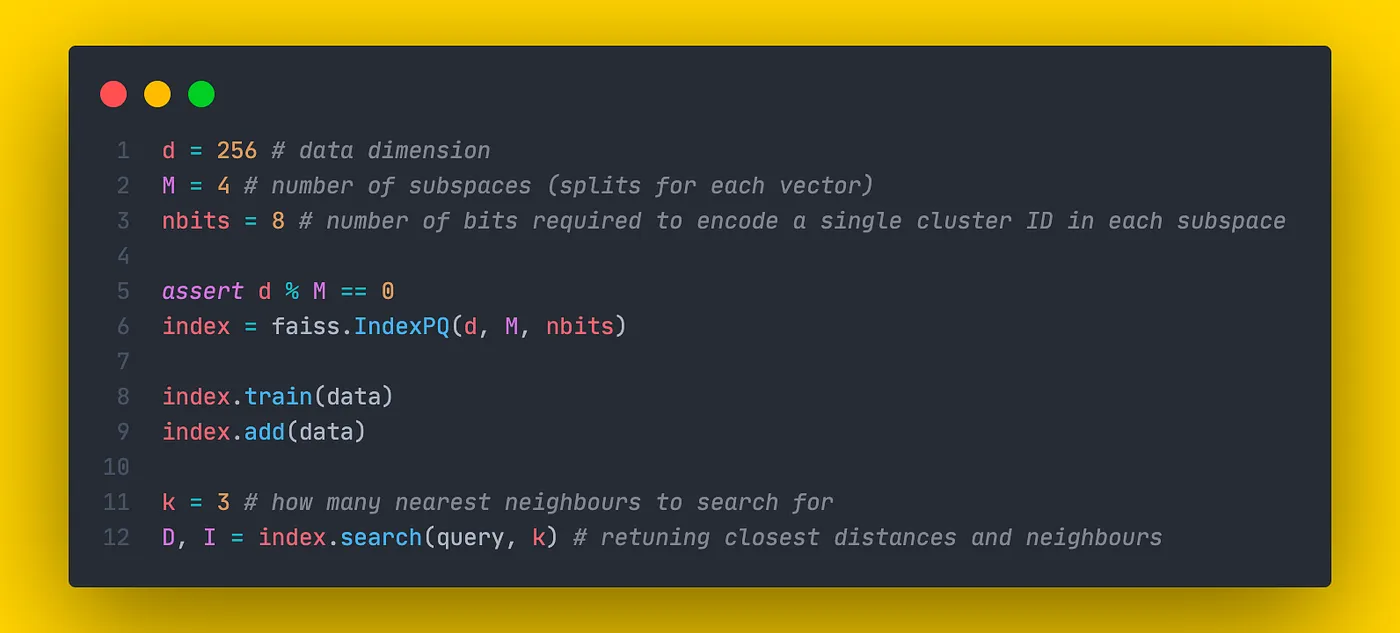
PQ 是在 IndexPQ 类中实现的。对于初始化,我们需要提供3个参数:
- d:数据维度
- M: 每个向量的分割数(与上面使用的 n 相同的参数)
- nbits: 编码单个集群 ID 所需的位数。这意味着一个子空间中的总簇数等于 $k = 2^{nbit}$。
对于等子空间维数分裂,参数 dim 必须被 M 整除。
存储单个向量所需的总字节数等于:
$bytes = \lceil \frac {M*nbits}{8} \rceil$
As we can see in the formula above, for more efficient memory usage the value of M * nbits should be divisible by 8.
结论
我们已经研究了一种在信息检索系统中非常流行的算法,它可以有效地压缩大量数据。其主要缺点是推理速度缓慢。尽管如此,该算法在现代大数据应用中得到了广泛应用,特别是与其他最近邻搜索技术相结合时。
参考
所有图像均来自 《Similarity Search, Part 2: Product Quantization》

